LoRA(Low Rank Adaption of LLM) explained

LoRA is a very famous technique known to people working with Large Language Models.

In this article we will deep dive with mathematics (Linear Algebra)understand what good it does!

There are 3 steps to understand LoRA.

1. Rank of a Matrix
2. Matrix Factorization (In this case Singular Value Decomposition or SVD in short)
3. Matrix approximation

What is Rank ?

Rank of a matrix is the number of linearly independent columns (or Rows).

If A is a mxn matrix , its rank(A)<=min(m,n)

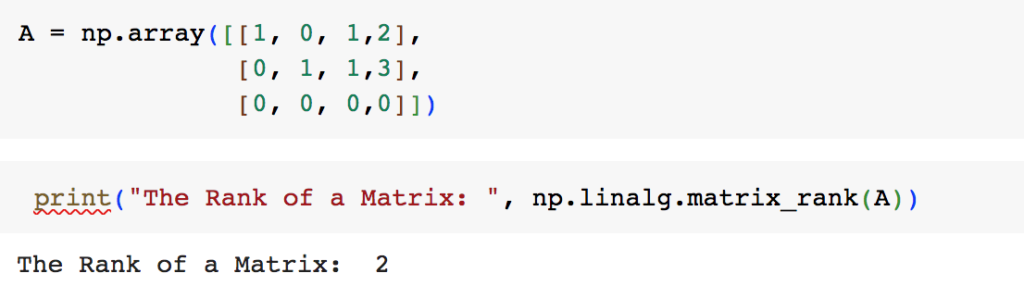
But what does Rank have to do with LoRA?

Let’s first understand Matrix Factorization.

Matrix factorization is splitting the matrix into 2 or more matrices.

e.g. A=B.C

Splitting Matrix A into B and C , so that their matrix multiplication produces A.

There are many methods available to do such matrix factorization. Singular Value Decomposition is one of them.

SVD

Any matrix of order (mxn)can be written as a matrix multiplication of 3 matrices as follows:

A=UΣV^T and rank of A is ‘r’

Where:

U is a mxm matrix

V is nxn matrix

Σ is a mxn matrix, the diagonal values of first ‘r’ rows are singular values of A and rest of the entries are zero.